sptSet[i] será true se o vértice fizer parte do menor caminho,
ou se não for possível continuar
Isso eu entendi, mas não faz sentido você usar uma wrapper class (Boolean) ao invés de um tipo primitivo (boolean).
alterei para o boolean primitivo, mas não estou conseguindo mostrar o caminho do vértice, só mostra o custo
Posta o seu código atualizado.
O programa deve solicitar ao usuário o vértice de partida da rota e o vértice de destino. Em seguida, deve descrever o menor trajeto possível do vértice de partida até o destino. Por exemplo, dado o vértice de partida 2 e o vértice de destino 4 para o grafo abaixo, o programa deve apresentar a saída 2 – 3 – 4.
import java.util.Scanner;
public class shortestPath {
static final int V = 9;
/* Encontra o vértice mais próximo do conjunto de vértices ainda não incluidos na árvore
de menor caminho */
int minDistance(int dist[], Boolean sptSet[]){
// Inicializa o menor valor
int min = Integer.MAX_VALUE, min_index = -1;
for (int v = 0; v < V; v++)
if (sptSet[v] == false && dist[v] <= min) {
min = dist[v];
min_index = v;
}
return min_index;
}
// Exibe o vetor distancia
void printSolution(int dist[]) {
System.out.println("Vertex \t\t Distance from Source");
for (int i = 0; i < V; i++)
System.out.println(i + " \t\t " + dist[i]);
}
// Imlementa o algoritmo
void dijkstra(int graph[][], int src) {
// Vetor que possui o resultado. Armazena a distância de cada vértice para a origem.
//dist[i] possuirá o menor caminho da origem até i.
int dist[] = new int[V];
//sptSet[i] será true se o vértice fizer parte do menor caminho
//ou se não for possível continuar
Boolean sptSet[] = new Boolean[V];
// Inicializa todas as distâncias com o maior valor possível
//e stpSet[] como false
for (int i = 0; i < V; i++) {
dist[i] = Integer.MAX_VALUE;
sptSet[i] = false;
}
// A distância de todo nó para si mesmo é zero
dist[src] = 0;
// Encontra o menor caminho para todos os vértices
for (int count = 0; count < V - 1; count++) {
/* Seleciona o vértice com menor distância dos vértices ainda não visitados.
*
* u sempre é a origem na primeira iteração.
*/
int u = minDistance(dist, sptSet);
// Marca o vértice como visitado
sptSet[u] = true;
/* Atualiza o valor dist dos vértices adjacentes ao vértice selecionado*/
for (int v = 0; v < V; v++)
/* Atualiza dist[v] apenas se ele não estiver em sptSet,
* existe uma aresta entre u e v, e o peso total do caminho da origem até
* o destino é menor do que o atual dist[v]
*/
if (!sptSet[v] && graph[u][v] != 0 && dist[u] != Integer.MAX_VALUE &&
dist[u] + graph[u][v] < dist[v])
dist[v] = dist[u] + graph[u][v];
}
// Exibe o vetor com as distâncias
printSolution(dist);
}
public static void main(String[] args) {
int graph [][] = new int[][] { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 4, 14, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 0, 0, 2, 0, 1, 6 },
{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
{ 0, 0, 2, 0, 0, 0, 6, 7, 0 } };
shortestPath t = new shortestPath();
Scanner scanner = new Scanner(System.in);
System.out.println("Digite a vértice de partida:");
int input = scanner.nextInt();
System.out.println("Digite a vértice de destino:");
input = scanner.nextInt();
t.dijkstra(graph, input);
//t.dijkstra(graph, 0) ;
scanner.close();
}
}
Ao ler o destino, você está matando o conteúdo da partida.
Mesmo assim seu código não faz sentido, pois você tem um array bidimensional, ou seja, uma matriz, então tanto a sua origem quanto o seu destino precisam ser uma coordenada representando a linha e a coluna do vértice. mas você só está lendo um número.
Outra coisa, seu tópico está duplicado no seguinte post:
Certo, então terei que criar uma coordenada
representando a linha e a coluna do vértice, como assim?
Olha só, você tem a seguinte matriz com 9 linhas e 9 colunas:
int[][] graph = new int[][] {
{ 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 4, 14, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 0, 0, 2, 0, 1, 6 },
{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
{ 0, 0, 2, 0, 0, 0, 6, 7, 0 }
};
Como é que você informa a posição inicial hoje?
Você só está lendo um número e armazenando numa variável input, mas esse input representa qual posição dessa matriz?
Se eu quiser iniciar a busca a partir da linha 2 coluna 5, e chegar até a linha 8 coluna 1, como eu faço?
Como é que você informa a posição inicial hoje? O método min_index vai retornar a primeira posição
Você só está lendo um número e armazenando numa variável input, mas esse input representa qual posição dessa matriz? Esse input é usado para usuário informar a posição
Se eu quiser iniciar a busca a partir da linha 2 coluna 5, e chegar até a linha 8 coluna 1, como eu faço? Essa parte não entendi
O que a sua matriz representa?
Então posta um exemplo de qual valor você informa e qual é a posição correspondente na matriz.
O que a sua matriz representa? Representa um grafo
Então posta um exemplo de qual valor você informa e qual é a posição correspondente na matriz.
Vértice de partida 2 e o vértice de destino 4
É uma matriz de adjacências.
Não olhei seu algoritmo com calma, mas pense o seguinte. Ao executar o algoritmo de Dijsktra para um grafo ponderado, o resultado esperado é uma árvore, ou seja, um grafo acíclico o que implica que existe um único caminho entre dois vértices contidos em um componente conexo. O seu primeiro problema é ver se o seu algoritmo funciona.
O segundo passo é gerar o caminho fonte-destino. A árvore gerada terá como raiz o vértice fonte e ramificará para os outros vértices. A partir do vértice destino, faça o caminho contrário buscando pela fonte. O armazenamento dessa árvore é feito, no seu caso (pelo menos me parece) no array dist.
Pois é, é o que me parece também, mas o colega insiste que é um grafo, mas nem ele sabe descrever como determinar o ponto de partida e de destino.
Acredito que o problema nem está no algoritmo mas sim em entender o que é um grafo e o que é uma matriz de adjacências.
Talvez faltou prestar mais atenção na aula.

É que uma matriz de adjacências é uma das formas de implementar um grafo.
Não tinha me tocado disso.
Não me faz sentido utilizar matriz de adjacências para representar um grafo uma linguagem com foco em programação orientada à objetos.
Mas essa é minha singela opinião.
Na verdade faz sentido dependendo do tipo do grafo. Grafos densos (altamente conectados), sem anomalias em arestas, são processados de forma mais “rápidos” se implementados usando matrizes de adjacências. Implementações de propósito geral realmente são implementados usando OO ou mesmo tabelas de símbolos. A biblioteca networkx em python, se não me engano, usa tabelas de símbolos.
O caso dele é algo mais didático, mas nesse ponto do campeonato, faz mais sentido usar um grafo implementado com listas de adjacências, pelo menos eu prefiro.
Sim, amigo algoritmo tá funcionando, o problema é que só mostra o custo, no caso a questão pede que usuário solicite a vértice de partida da rota e o
vértice de destino e em seguida descrever o menor
trajeto possível do vértice de partida até o destino. Obrigado pela ajuda!
Dei uma mexida pra poder ajudar, beleza? O que falta para você é um array para armazenar a árvore gerada. Veja aí na minha versão, se chama edgeTo (aresta até). Tirei seus comentários pra ficar mais enxuto. Coloquei mais dois métodos para verificar se há um caminho entre dois vértices após o processamento (a raiz ficará com -1) e um método para obter o caminho, que no caso, caminha dentro do edgeTo. Vou anexar um desenho que fiz tbm pra vc.
import java.util.ArrayDeque;
import java.util.Deque;
import java.util.Scanner;
/**
*
* @author david
*/
public class CaminhoMinimo {
private int V = 10;
private int[] dist;
private int[] edgeTo;
private boolean[] sptSet;
public CaminhoMinimo( int[][] graph, int src ) {
dijkstra( graph, src );
}
private int minDistance( int dist[], boolean sptSet[] ) {
int min = Integer.MAX_VALUE, min_index = -1;
for ( int v = 0; v < V; v++ ) {
if ( sptSet[v] == false && dist[v] <= min ) {
min = dist[v];
min_index = v;
}
}
return min_index;
}
private void printSolution() {
System.out.println( "Vertex \t Distance from Source \t Edge To" );
for ( int i = 0; i < V; i++ ) {
System.out.println( i + " \t " + dist[i] + " \t\t\t " + edgeTo[i] );
}
}
private void dijkstra( int[][] graph, int src ) {
V = graph.length;
dist = new int[V];
edgeTo = new int[V];
sptSet = new boolean[V];
for ( int i = 0; i < V; i++ ) {
dist[i] = Integer.MAX_VALUE;
edgeTo[i] = -1;
sptSet[i] = false;
}
dist[src] = 0;
for ( int count = 0; count < V - 1; count++ ) {
int u = minDistance( dist, sptSet );
sptSet[u] = true;
for ( int v = 0; v < V; v++ ) {
if ( !sptSet[v] &&
graph[u][v] != 0 &&
dist[u] != Integer.MAX_VALUE &&
dist[u] + graph[u][v] < dist[v] ) {
dist[v] = dist[u] + graph[u][v];
edgeTo[v] = u;
}
}
}
printSolution();
}
private boolean hasPathTo( int v ) {
return dist[v] < Integer.MAX_VALUE;
}
public Iterable<Integer> pathTo( int v ) throws IllegalArgumentException {
if ( !hasPathTo( v ) ) {
return null;
}
Deque<Integer> path = new ArrayDeque<>();
for ( int atual = v; atual != -1; atual = edgeTo[atual] ) {
path.push( atual );
}
return path;
}
public static void main( String[] args ) {
int[][] graph = new int[][]{
{ 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 4, 14, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 0, 0, 2, 0, 1, 6 },
{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
{ 0, 0, 2, 0, 0, 0, 6, 7, 0 }
};
Scanner scanner = new Scanner( System.in );
System.out.println( "Digite o vértice fonte:" );
int input = scanner.nextInt();
CaminhoMinimo t = new CaminhoMinimo( graph, input );
System.out.println( "Digite o vértice de destino:" );
input = scanner.nextInt();
scanner.close();
boolean first = true;
for ( int v : t.pathTo( input ) ) {
if ( !first ) {
System.out.print( " -> " );
}
System.out.print( v );
first = false;
}
System.out.println();
}
}
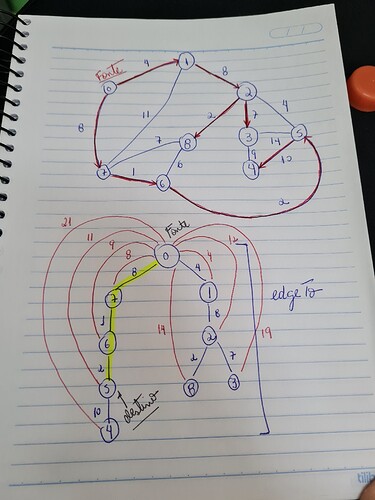
Os desenhos estão fora de escala. Primeiro eu desenhei o grafo, passei a limpo (em cima). Em vermelho está o resultado da árvore gerada. Embaixo é a representação do array edgeTo e os arcos em vermelho são as distâncias somadas das arestas da fonte até o destino. No meu exemplo usei 0 como fonte e 5 como destino.
Veja a entrada:
Digite a vértice de partida:
0
Vertex Distance from Source Edge To
0 0 -1
1 4 0
2 12 1
3 19 2
4 21 5
5 11 6
6 9 7
7 8 0
8 14 2
Digite a vértice de destino:
5
0 -> 7 -> 6 -> 5
Muito obrigado pela ajuda  , agora estou entendendo a logica do algoritmo
, agora estou entendendo a logica do algoritmo