Preciso de ajuda nesse codigo que implementa o algoritmo de Dijkstra (Grafo):

Programação Java
,
#22

Na verdade faz sentido dependendo do tipo do grafo. Grafos densos (altamente conectados), sem anomalias em arestas, são processados de forma mais “rápidos” se implementados usando matrizes de adjacências. Implementações de propósito geral realmente são implementados usando OO ou mesmo tabelas de símbolos. A biblioteca networkx em python, se não me engano, usa tabelas de símbolos.

O caso dele é algo mais didático, mas nesse ponto do campeonato, faz mais sentido usar um grafo implementado com listas de adjacências, pelo menos eu prefiro.

#23

Sim, amigo algoritmo tá funcionando, o problema é que só mostra o custo, no caso a questão pede que usuário solicite a vértice de partida da rota e o
vértice de destino e em seguida descrever o menor
trajeto possível do vértice de partida até o destino. Obrigado pela ajuda!

#24

Dei uma mexida pra poder ajudar, beleza? O que falta para você é um array para armazenar a árvore gerada. Veja aí na minha versão, se chama edgeTo (aresta até). Tirei seus comentários pra ficar mais enxuto. Coloquei mais dois métodos para verificar se há um caminho entre dois vértices após o processamento (a raiz ficará com -1) e um método para obter o caminho, que no caso, caminha dentro do edgeTo. Vou anexar um desenho que fiz tbm pra vc.

import java.util.ArrayDeque;
import java.util.Deque;
import java.util.Scanner;

/**
 *
 * @author david
 */
public class CaminhoMinimo {

    private int V = 10;
    private int[] dist;
    private int[] edgeTo;
    private boolean[] sptSet;

    public CaminhoMinimo( int[][] graph, int src ) {
        dijkstra( graph, src );
    }
    
    private int minDistance( int dist[], boolean sptSet[] ) {

        int min = Integer.MAX_VALUE, min_index = -1;

        for ( int v = 0; v < V; v++ ) {
            if ( sptSet[v] == false && dist[v] <= min ) {
                min = dist[v];
                min_index = v;
            }
        }

        return min_index;

    }

    private void printSolution() {
        System.out.println( "Vertex \t Distance from Source \t Edge To" );
        for ( int i = 0; i < V; i++ ) {
            System.out.println( i + " \t " + dist[i] + " \t\t\t " + edgeTo[i] );
        }
    }

    private void dijkstra( int[][] graph, int src ) {

        V = graph.length;

        dist = new int[V];
        edgeTo = new int[V];
        sptSet = new boolean[V];

        for ( int i = 0; i < V; i++ ) {
            dist[i] = Integer.MAX_VALUE;
            edgeTo[i] = -1;
            sptSet[i] = false;
        }

        dist[src] = 0;

        for ( int count = 0; count < V - 1; count++ ) {

            int u = minDistance( dist, sptSet );
            sptSet[u] = true;

            for ( int v = 0; v < V; v++ ) {
                if ( !sptSet[v] && 
                     graph[u][v] != 0 && 
                     dist[u] != Integer.MAX_VALUE &&
                     dist[u] + graph[u][v] < dist[v] ) {
                    
                    dist[v] = dist[u] + graph[u][v];
                    edgeTo[v] = u;
                }
            }
        }

        printSolution();

    }

    private boolean hasPathTo( int v ) {
        return dist[v] < Integer.MAX_VALUE;
    }
    
    public Iterable<Integer> pathTo( int v ) throws IllegalArgumentException {
        
        if ( !hasPathTo( v ) ) {
            return null;
        }
        
        Deque<Integer> path = new ArrayDeque<>();
        
        for ( int atual = v; atual != -1; atual = edgeTo[atual] ) {
            path.push( atual );
        }
        
        return path;
        
    }
    
    public static void main( String[] args ) {

        int[][] graph = new int[][]{
            { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
            { 4, 0, 8, 0, 0, 0, 0, 11, 0 },
            { 0, 8, 0, 7, 0, 4, 0, 0, 2 },
            { 0, 0, 7, 0, 9, 14, 0, 0, 0 },
            { 0, 0, 0, 9, 0, 10, 0, 0, 0 },
            { 0, 0, 4, 14, 10, 0, 2, 0, 0 },
            { 0, 0, 0, 0, 0, 2, 0, 1, 6 },
            { 8, 11, 0, 0, 0, 0, 1, 0, 7 },
            { 0, 0, 2, 0, 0, 0, 6, 7, 0 }
        };

        Scanner scanner = new Scanner( System.in );
        System.out.println( "Digite o vértice fonte:" );
        int input = scanner.nextInt();

        CaminhoMinimo t = new CaminhoMinimo( graph, input );

        System.out.println( "Digite o vértice de destino:" );
        input = scanner.nextInt();
        
        scanner.close();
        
        boolean first = true;
        
        for ( int v : t.pathTo( input ) ) {
            
            if ( !first ) {
                System.out.print( " -> " );
            }
            
            System.out.print( v );
            first = false;
            
        }
        System.out.println();

    }

}

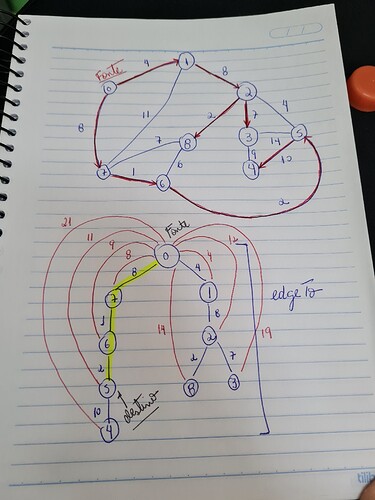
20220217_142629
20220217_142629908×1209 235 KB

Os desenhos estão fora de escala. Primeiro eu desenhei o grafo, passei a limpo (em cima). Em vermelho está o resultado da árvore gerada. Embaixo é a representação do array edgeTo e os arcos em vermelho são as distâncias somadas das arestas da fonte até o destino. No meu exemplo usei 0 como fonte e 5 como destino.

Veja a entrada:

Digite a vértice de partida:
0
Vertex    Distance from Source    Edge To
0         0                       -1
1         4                       0
2         12                      1
3         19                      2
4         21                      5
5         11                      6
6         9                       7
7         8                       0
8         14                      2
Digite a vértice de destino:
5
0 -> 7 -> 6 -> 5
2 curtidas
#25

Muito obrigado pela ajuda :heart:, agora estou entendendo a logica do algoritmo

1 curtida
#26

No exemplo apresentado, o menor caminho de 2 para 4 não é 2-3-4 (16) mas sim 2-5-4 (14)