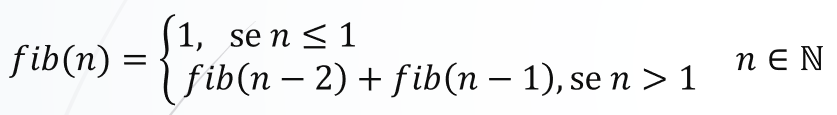Olá, eu estou estudando recursividade e gostaria de discutir sobre o assunto, trazendo pontos que eu quero saber de vocês se estou correto ou errei no raciocínio.
- O primeiro raciocínio (e único) foi um programa utilizando uma função recursiva para descobrir o número x da sequência Fibonacci no seguinte trecho de código (meio portugol):
função Fibonacci( inteiro x)
{
se x = 1 ou x = 0
retorne x
senão
retorne Fibonacci(x-1) + Fibonacci(x-2)
}
O meu ponto é nas ramificações que isso gera, eu entendi recursividade de maneira conceitual, consigo em python ou em C escrever um algoritmo que calcule fatorial de qualquer número, porém quando me deparei com a questão de fibonacci simplesmente não saí do lugar. Até ver o algoritmo acima.
Vou deixar um PDF com as ramificações que eu fiz para que vocês entendam melhor sobre o que eu estou falando.
Fibonacci.pdf (582,2,KB)
Está correto este raciocínio?
Com o que eu acho que entendi de funções acho que sim. Foi realmente um divisor de águas pra mim, eu seguia antes uma linha de recursões sem ramificações. A abstração ao imaginar um número grande na sequência fibonacci é algo que é difícil para eu assimilar mesmo entendendo o conceito. Alguém teria uma ideia de como eu posso descrever essas ramificações matemáticamente?
Se puderem deixar sugestões de outras aplicações de recursividade, outras abstrações com este método, eu agradeceria.
Obrigado.
Sim, seu raciocínio está correto. Só vale lembrar que quando chega em Fibonacci(1) e Fibonacci(0), ele entra no se x = 1 ou x = 0.
Mas vale lembrar que Fibonacci recursivo é o pior e mais ineficiente jeito de resolver o problema. Isso porque são geradas muitas chamadas redundantes.
Por exemplo, se F for a sua função recursiva, chamar F(10) faz o seguinte:
F(10) = F(9) + F(8)
F(10) = F(8) + F(7) + F(7) + F(6)
F(10) = F(7) + F(6) + F(6) + F(5) + F(6) + F(5) + F(5) + F(4)
....
Repare que F(8) é calculada duas vezes, F(7) 3 vezes, e assim por diante. Quanto maior o número inicial, mais chamadas recursivas - e neste caso, redundantes - serão feitas, e isso cresce exponencialmente conforme o valor inicial.
Recursão é um conceito importante e deve ser aprendido, mas mais importante ainda é saber quando não usar. No caso de Fibonacci, o pessoal usa pra ensinar porque a definição matemática é recursiva e parece que fica mais “didático”. Mas ao transpor isso para código, se torna uma solução ruim, e um loop resolve de maneira muito melhor e mais simples.
2 curtidas
Pra entender recursividade, primeiro você precisa entender recursividade.
2 curtidas
Sem dúvida a forma iterativa de se resolver esse problema é melhor. Como você falou, é didática, eu já tinha lido que a recursão muita das vezes pode deixar o código mais bonito de se ver porém pode não ser eficiente, não tinha ainda entendido, mas no exemplo de fibonacci, consigo ver que a recursão não é a melhor estratégia. Mesmo assim, achei bem interessante o fato de cada chamada da função fazer mais 2 chamadas recursivas. Obrigado novamente!
Só parece algo do outro mundo, mas não é. É a base da computação e como uma prova formal por indução funciona na matemática. A forma de se descrever uma recursão matematicamente é chamada de fórmula de recorrência, relação de recorrência ou só recorrência, que é quando na definição de uma função a própria função aparece novamente. É algo que é definido em termos de si mesmo. Fibonacci ficaria algo como:
Além disso, existem diversos tipos de recursão dependendo do contexto. Simples, composta, direta, indireta, mais à esquerda, mais à direita…
1 curtida
Interessante consegui entender. Eu estou no segundo ano de faculdade e minha matemática de escola foi muito fraca mas consigo visualizar nessa descrição matemática o funcionamento do algoritmo que eu deixei acima. Uma das primeiras coisas que ganhou sentido pra mim quando entrei na faculdade foi a aplicabilidade de funções, que na escola eu não via sentido. Obrigado pela resposta, não sabia dos outros tipos de recursão vou dar uma estudada depois.
Infelizmente o ensino básico no nosso país é um lixo, salvo escolas federais ou particulares. Claro que os alunos tem que querer ir atrás tbm, mas se vc não tem um professor que consegue ensinar o básico de forma minimamente decente, fica difícil ter vontade ou alguma motivação para ir aprender mais. Continue assim.
2 curtidas