Olá alguém aí sabe como que eu faço para
representar grafos em java, com algum exemplo
de código? Eu tenho q fazer um trabalho e o Livro do Níviio Ziviani
não esta me ajudando muito.
pô véi, montas as estruturas é bem simples, foda mesmo são os algoritmos hehe
class Grafo
{
List<Nodo> nodos; // todos os vértices do grafo
}
class Nodo
{
class Incidencia
{
Nodo nodo; // referência ao nodo adjacente
int peso; // valor da aresta
}
List<Incidencia> incidencias;
}bom, isso aí é a estrutura bem básica mesmo, daí se vc quiser acrescenta outras informações e claro, escreve as funções que manipulam os vértices
espero ter ajudado
qlqr duvida tamo ae
flw, t+
Ow véio valeu pela ajuda agora eu tô tentando entender os algoritmos do nívio Ziviani msm,
já tô implementando aqui tá dando uns erro aqui na hora de inserir as arestas.
HAUHAUAHUHAUUAA, sera que as faculdades seguem o mesmo padrão? ou a mesma apostilinha? jahuahuhuaha eu tive exatamente isso o ano passado e foi uns dos trabalhinhos mais gostosos que eu ja fiz…
cara tenho isso pronto em casa acho que não seria legal te mandar pronto pois o interessante e vc aprender mas oso te mandar se quizer manda o email…
Conselho se eu não me lembro vc tera arestas e vertices cada 1 e um objeto certo? crie beans para elas tipo Aresta possui um ponto x e um ponto y e o seu valor, vertices possuem tamanho, e localização x e y tbm…assim monte seus objetos e começa a manupula- los
Você pode representá-los através de matrizes também, com as colunas representado os vértices e as linhas representando as arestas:
//grafo com 4 nós e 3 arestas
int[][] grafo = { { 3 , 3 , 0 , 0 },
{ 0 , 2 , 2 , 0 },
{ 0 , 4, 4 , 0 } };
//encapsule-a em uma classe
class Grafo
{
public void adicionaVertice();
public void adicionaAresta();
//etc ....
}n entendi???
rmendes08, uma matriz de adjacências é muito mais simples de se trabalhar, implementar e entender, porém gasta mais memória e ainda torna a ordem de complexidade do problema maior, oq o deixa mais lento em relação à matriz de incidência
[quote=“TeiTei”]HAUHAUAHUHAUUAA, sera que as faculdades seguem o mesmo padrão? ou a mesma apostilinha? jahuahuhuaha eu tive exatamente isso o ano passado e foi uns dos trabalhinhos mais gostosos que eu ja fiz… [/quote]sei lá, mas os problemas básicos de grafos são sempre os mesmos, e sempre tem gente que pira pra entender um algoritmo de menor caminho (dijkstra e floyd), árvore geradora mínima (prim e kruskal) etc
Neste exemplo, o vértice 0 e o vértice 1 são conectados pela aresta 0, de peso 3. Os vértices 1 e 2 são conectados pelas arestas 1 e 2, de peso 2 e 4 respectivamente. O vértice 2 está isolado, pois não há nenhuma aresta associada. Neste caso eu coloquei os vértices nas colunas e as arestas nas linhas, pesquisando mais um pouco e vi que o usual é os vértices nas linhas e as arestas nas colunas (bem, já faz um tempinho que eu cumpri a disciplina  )
)
Um problema com a matriz de adjacência é que não é possível representar arestas de pesos diferentes para o mesmo par de vértices
é possível sim, só vc usar os índices da matriz pra dizer qual vértice se conecta a qual, e os valores dos índices pro peso, poe exemplo um grafo bidirecinal:
int grafo[][] = {
{ 0, 2, 0, 5, },
{ 2, 0, 3, 1, },
{ 0, 3, 0, 0, },
{ 5, 1, 0, 0, }, };nesse caso, ‘grafo[0][1]’ significa que o grafo ‘0’ é adjacente ao grafo ‘1’, e o valor da aresta é 2, da mesma forma, como o grafo é bidirecional então ‘grafo[1][0]’ representa a mesma coisa
as posições que possuem valor ‘0’ indica que ñ há adjacência, inclusive grafo[0][0], grafo[1][1] etc ñ possuem adjacência (grafo sem loop)
agora um grafo unidirecional:
int grafo[][] = {
{ 0, 2, 0, 5, },
{ 0, 0, 1, 1, },
{ 0, 3, 0, 0, },
{ 2, 0, 3, 0, }, };agora ‘grafo[0][1]’ significa o mesmo que no caso anterior, entretanto ñ tem como vc ir de ‘1’ até ‘0’, e pra ir de ‘0’ a ‘3’ o peso é 5, mas de ‘3’ a ‘0’ o peso é 2
como eu tava dizendo, é bem fácil, mas quanto maior o grafo menos eficiente vai ser, ainda mais no grafo bidirecional onde a matriz fica espelhada, deixando dados redundantes
mas é isso ae, num é ruim aprender a lidar com grafos a matriz d adjacência, é até aconselhável, mas depois de aprender os algoritmos seria bom aprender a melhorar as estruturas de dados
flw, t+
Então como você representaria, em uma matriz de adjacências, três arestas, uma de peso 2, outra de peso 3 e outra de peso 5?
mas tá faltando informação, essas arestas precisam ligar vértices, tudo bem q são 3 arestas, mas são quantos vértices? qual se liga a qual? formula a pergunta melhor q eu t explico
flw, t+
Então como você representaria, em uma matriz de adjacências, três arestas de um grafo bidirecional, uma de peso 2, outra de peso 3 e outra de peso 5 que ligam o mesmo par de vértices?
//exemplo pela matriz de incidências ( vértices nas linhas e arestas nas colunas )
int[][] grafo = {
{ 2 , 3 , 5, 0},
{ 2 , 3 , 5, 1},
{ 0 , 0 , 0, 1}
}
//os vértices 0 e 1 estão ligados pelas arestas 0, de peso 2, 1 de peso 3 e 2 peso 5.
//o vértice 2 está ligado ao vértice 1 pela aresta 2 de peso 1.Como representá-lo em uma matriz de ajacências ?
agora saquei, o grafo teria arestas duplicadas, realmente aí ñ tem jeito mesmo, independente de ser unidirecional ou bidirecional, mas se vc ñ usar uma matriz de inteiros, e usar uma matriz de uma estrutura de dados apropriada pra isso teria jeito sim, como no exemplo lá em cima
ou simplesmente ignore as arestas de peso maior hehe, se vc tem a opção de usar dois caminhos, um de peso 2 e ou de peso 3, então vc sempre usará o de peso 2, claro q pode haver complicações e em determinadas situações ela deverá ser contada, mas até lá…
é sempre melhor usar as incidências…
inté
Bem, acho que o tópico foi mais do que respondido. Resumindo: pode-se representar o grafo por matriz de adjacências, matriz de incidências, lista de incidências, etc. Qual a melhor? Aí depende do seu problema … nem sempre você vai precisar implementar a representação mais elaborada.
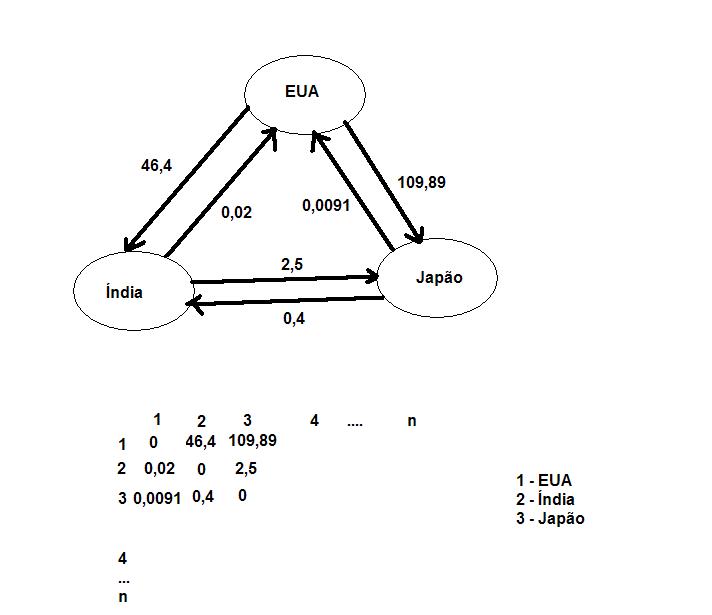
Entaum eu tô com um problema que é: resumidamente eu tenho vamos supor 1 dólar(EUA) compra 46,4 rúpias indianas e 1 rúpia indiana compra a 2,5 iênes japonês e 1 iênes japonês compra 0,0091 dolares, ou seja 46,42,50,0091 = 1,0556, o q corresponde a um lucro de 5,56% simplificadamente se eu tiver um dólar e sair comprando estas outras moedas no final das contas eu vou ter 1,05 dólares: o q eu pensei está em anexo o problema é q eu ñ tô sabendo direito usar as estrutura de grafos em java, e como representar em java o que eu pensei. Alguém pode me ajudar?
Meu programa receberá um arquivo de entrada, enumerando pré-requisitos. O arquivo contém:
número de matérias, na primeira linha; pré-requisito e matérias, nas demais linhas. um exemplo de arquivo de entrada (a matéria 0, por exemplo, é pré-requisito de 1 e 4). A entrada é esta:
6
0 1 4
1 2
2
3 2 5
4 1 5
5 2
Como que faço para produzir um arquivo com a ordenação Topologica correta das matérias, observando os
pré-requisitos? é um exercício de revisão de prova preciso de pelo menos uma ideia, Ajuda aí moçada.
Só sei que a saída deve ficar assim:::
3 0 4 5 1 2
Qualquer dica será e grande Importancia!!! VAlew
Boa semana!!
pra representar é só usar a estrutura q eu postei, agora o seu problema é bem foda, me parece uma variação do problema do caixeiro viajante, onde vc tem que percorrer todos os vértice s voltar para o anterior achando o menor caminho
no seu caso nem precisaria percorrer percorrer todos os vértices, apenas achar o maior caminho (ou o caminho mais valioso) entre um vértice e outro (podendo a origem e o destino ser o mesmo vértice)
pois então, a dica tá ae, constrói esse algoritmo e cerca essas condições q eu disse, e na medida q forem vindo dúvidas vá postando
e boa sorte, vai precisa hehe, flw, t+
oi galera !!!
alguem pode me ajudar :?: 
eu tenho um exercicio pq tenho um duvido 
exercicio uma pergunta la em baixo:
:arrow: 1) Leia um grafo, conforme mostrado na aula de laboratorio, e liste todos os vizinhos de um vertice.
:arrow: 2) Leia um grafo, conforme mostrado na aula de laboratorio, e liste o grau de todos os vertices do grafo.
:arrow: 3) Leia um grafo, conforme mostrado na aula de laboratorio, e liste e mostre se o grafo e euleriano.
Como fazer isso??? por favor, faz pra mim ai. 
abraçosss pra ti